Wydaje się, że niektóre odpowiedzi mówią, że chcesz, aby ciało rezonowało z częstotliwością dźwięku, aby wytworzyć maksymalną amplitudę dźwięku. To nie jest w porządku. Poniższy wykres przedstawia pomiar krzywej rezonansu skrzypiec Stradivarius z 1713 roku (przerysowany przeze mnie na podstawie rysunku Carleen Hutchins). Istnieje wiele różnych szczytów rezonansu, niektóre są mocne, a inne słabe; te w pobliżu 200 i 400 Hz to wibracje drewna, a te w pobliżu 300 Hz to rezonans powietrza wlatującego i wychodzącego przez otwory F. Białe linie pokazują podstawowe częstotliwości czterech strun.
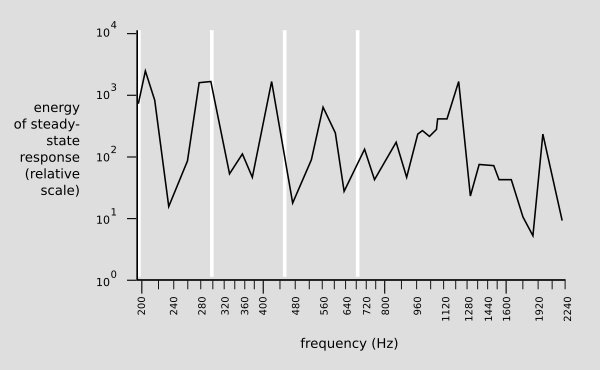
Więc możesz zobaczyć, że na pewno są piki, które wskazują na rezonanse, ale są raczej wąskie i jest ich dużo. Z tego, co niewiele rozumiem z akustyki skrzypiec, wpływ na dźwięk jest skomplikowany i wiąże się ze sposobem, w jaki różne harmoniczne pokrywają się z wieloma różnymi rezonansami. Kiedy grasz z vibrato, przesuwasz harmoniczne tam iz powrotem po tych szczytach rezonansu. W każdym razie nie jest to sytuacja, w której podstawowa częstotliwość nuty po prostu pasuje do częstotliwości rezonansowej ciała i / lub jamy powietrznej.
OP konkretnie pyta:
Dlaczego instrumenty strunowe o niższym tonie mają większy korpus?
Innymi słowy, dlaczego nie możemy mieć kontrabasu z płytą rezonansową wielkości skrzypiec? Odpowiedź ma tak naprawdę mniej wspólnego z rezonansem ciała niż z rozmiarem ciała w stosunku do wielkości fal dźwiękowych. Każdy ze szczytów rezonansu na powyższym wykresie odpowiada pewnemu wzorowi wibracji płyty rezonansowej. Poniżej znajduje się kilka diagramów z WP, przedstawiających wzorce drgań płyty rezonansowej gitary.
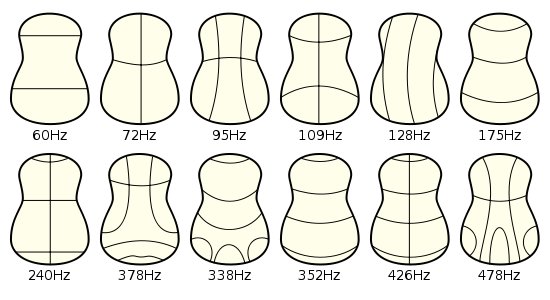
Kluczową kwestią jest to, że we wszystkich tych wzorcach niektóre obszary rosną, a inne spadają. Oznacza to, że różne części płyty rezonansowej mają różne fazy. Teraz najniższą nutą, jaką można zagrać na kontrabasie, jest 41 Hz, co odpowiada długości fali 800 cm. Załóżmy, że próbujesz wydobyć ten dźwięk za pomocą płyty rezonansowej wielkości skrzypiec, w której różne wibrujące łaty miały tylko 5–10 cm. Następnie dla każdego obszaru, który wibruje na zewnątrz, próbując wytworzyć nadciśnienie w powietrzu, w pobliżu znajdowałaby się kolejna łata, która jednocześnie wibruje do wewnątrz, próbując wytworzyć podciśnienie. Nie współpracują. Będą bardzo blisko anulowania.
Odnieśmy się do łaty, która próbuje wytworzyć nadciśnienie jako +, a druga jako -. Idealnie byłoby, gdyby łata + i łatka - były oddalone od siebie o 400 cm. Byłoby to pół długości fali, a wtedy + i - faktycznie współpracowałyby przy wytwarzaniu tej samej fali sinusoidalnej o długości 800 cm: jeden wytwarzałby grzbiet, a drugi wytwarzałby dolinę.
W rzeczywistości, wielkość płyty rezonansowej kontrabasu znajduje się gdzieś pomiędzy tymi dwoma skrajnościami. Ponieważ jest dość mały w porównaniu z większością odtwarzanych długości fal, jest dużo anulowania i niewielka współpraca. Jednak anulowanie nie jest idealne, więc masz trochę dźwięku. Instrument można zwiększyć głośniej, zwiększając go, ale byłoby to niepraktyczne.